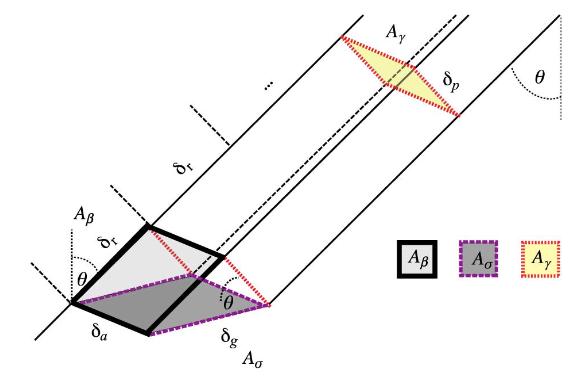
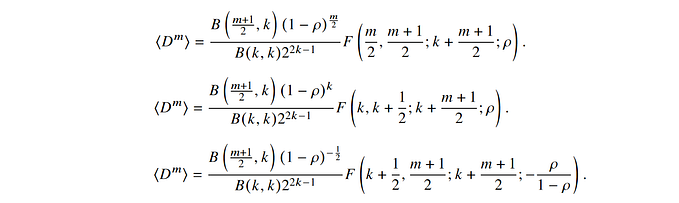How to oversample an SLC radar image properly?

By verifying that the center of the spectrum is at the extremities

An SLC image does not have classical statistics, as we saw here.
To oversample it as cleanly as possible, it is a matter of operating on the complex spectrum, adding zeros around it, and then doing the reverse ifft. In itself, this operation is not too complicated, but it still requires vigilance:

• in python, as in matlab, the maximum frequency of the spectrum is not in the middle of the image or the axis, but on the extremities.
• in the case of spotlight images, the physical center of the spectrum moves in distance: it will not be the same for different azimuths, because the antenna is depointed.

In practice, this means that the first operation is to find the center of the spectrum and make sure that it is at the extremities. If this is not the case, as in the slightly more complicated spotlight case, we will see later how to find this center of spectrum from the metadata.

We illustrate the steps on an image of TerraSAR-X/Tandem-X image of Toulouse (France), generously acquired by the DLR (scientific proposal OTHER0103). We select a small extract of 200 x 200 pixels for our example.
Let’s not forget that to display it, it is better to display the thresholded amplitude, as already detailed here.

plt.figure(figsize=(4,3))
plt.imshow(np.abs(Z),vmin=0,vmax=350,cmap='gray')

If we observe the shape of its spectrum, we see that it is not centered: the horizontal black band is not in the middle.

plt.figure()
plt.imshow(np.abs(np.fft.fft2(Z)),vmin=0,vmax=1e5,cmap='gray')

So the very first step is to find the center of the spectrum and shift that spectrum according to this center. This can be done either from the metadata or algorithmically. In the latter case, we propose the following lines of code to estimate the position Ix and Iy of the minimum of the spectrum signal.

def center_spectrum_2D(A):
    F=np.fft.fft2(A) # Fourier spectrum
    Bx=np.mean(np.abs(F),axis=0) # horizontal axis
    By=np.mean(np.abs(F),axis=1) # vertical axis
    
    Nx=np.size(Bx)
    Mx=Nx//8
    if (Mx % 2) == 0:
        Mx=Mx+1
    
    Ny=np.size(By)
    My=Ny//8
    if (My % 2) == 0:
        My=My+1
    
    Bxx = savgol_filter(Bx, Mx, 3)
    Byy = savgol_filter(By, My, 3)
    
    rx = np.where(Bxx==np.min(Bxx))
    ry = np.where(Byy==np.min(Byy))
    Ix=(rx[0][0])
    Iy=(ry[0][0])
    
    return Iy,Ix

And to shift the spectrum:

def Apply_center_spectrum(Z,Ix,Iy):
    #Ix,Iy=center_spectrum_2D(Z)
    nx,ny=np.shape(Z)
   
    Zc=np.fft.ifft2(np.roll(np.fft.fft2(Z),-nx//2-Iy,axis=1))
    Zc=np.fft.ifft2(np.roll(np.fft.fft2(Z),-ny//2-Ix,axis=0))
   
    return Zc

If we call Zc the complex matrix whose spectrum will be recentered, we simply apply:

Ix,Iy=center_spectrum_2D(Z)
Zc=Apply_center_spectrum(Z,Ix,Iy)

The spectrum is now like this:

We can then pad the spectrum with as many zeros as necessary to obtain a spectrum of the size of the final image that we want to obtain.
This can be done with the following function:

def upsampling_padding_spectrum_2D(A,mx,my):
    nx,ny=np.shape(A)
    # Check mx>nx,my>ny
    if mx < nx:
        raise ValueError("Number of final raws must be higher or equal than initial raws")
    if my < ny:
        raise ValueError("Number of final columns must be higher or equal than initial columns")
    
    F=np.fft.fft2(A) # Compute Spectrum
    #Ix,Iy=center_spectrum_2D(A) # Find Spectrum Center
    Ix=nx//2
    Iy=ny//2

    Fupsample=np.zeros((mx,my),dtype=np.complex64)
    
    Fupsample[0:Ix,0:Iy]=F[0:Ix,0:Iy]
    Fupsample[(mx-nx+Ix):mx,0:Iy]  =F[Ix:nx,0:Iy]
    Fupsample[0:Ix,(my-ny+Iy):my]  =F[0:Ix,Iy:ny]
    Fupsample[(mx-nx+Ix):mx,(my-ny+Iy):my]  =F[Ix:nx,Iy:ny]

    Apad=np.fft.ifft2(Fupsample)*mx*my/nx/ny
    return Apad

In this way, the speckle statistics are completely preserved.
This can be seen by zooming in on bright spots, or speckle dots:

Left : Zoom on the initial image / Right: Zoom on the up-sampled image

If you want to use this complex oversampled image later, and combine it with other images of the same type, do not forget to shift the spectrum again back, with the original offset.

def desApplycenter_spectrum(Z,Ix,Iy):
    nx,ny=np.shape(Z)
   
    Zc=np.fft.ifft2(np.roll(np.fft.fft2(Z),+nx//2+Iy,axis=1))
    Zc=np.fft.ifft2(np.roll(np.fft.fft2(Z),+ny//2+Ix,axis=0))
    return Zc

Reasoning by keeping the maximum spectrum on the matrix edges is a trick that then allows to come back to the initial position easily, without reasoning on the parity or on the resampling factor!

Bottom line:
● The oversampling operations of a complex signal are done by padding zeros in the Fourier domain, in order to preserve the statistics of the speckle.
● In the case of a spotlight acquisition, it is necessary to take care of the fact that by default, the center of the spectrum is not at the edges of the signal support.